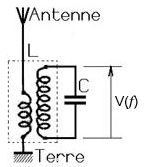
environnanteset les injecte dans le circuit gauche du transformateur. Seuls les signaux dont la fréquence sera proche de \(f_0\) seront présent aux bornes de \(C\). En règle générale, \(L\) est fixe. \(L\) est l'inductance que
voitle condensateur \(C\). \(C\) est variable est permet à l'utilisateur du poste de sélectionner la station de son choix.
Exemple
En effet, dans beaucoup de postes radio TSF, \(C\) est compris entre 30 pF et 500 pF; et \(L\) vaut souvent 170 µH pour la gamme des petites ondes ( PO ).
Un outil de calcul, bien pratique, vous est proposée ci-contre.
Les stations de radio captées par les TSF sont réparties dans des espaces de fréquence appelés bandes. La gamme des ondes radio se divisent en bandes et sous bandes. Une liste de celles-ci est donnée fig.2 . La bande dite FM est la plus récente. Elle est réservée aux émissions en modulation de fréquence. C’est le mode qui donne les meilleurs résultats de restitution du son. Seule cette bande pouvait prétendre, jusqu’à il y a peu de temps, à une écoute en haute-fidélité (HiFi). Le nouveau procédé de codage numérique DRM vient bousculer cet état de fait.
Les 3 bandes AM sont réservées aux émissions en modulations d’amplitude. Elles sont apparues à l’aube de la TSF. Les stations qui émettent dans les bandes PO et surtout OC bénéficient, à la nuit tombée, d’une portée améliorée.
Les grandes ondes sont inconnues aux USA.
BANDE |
S/BANDE |
SIGLE |
FMin |
FMax |
AM (*) |
Grandes Ondes |
GO |
150KHz |
525KHz |
Petites Ondes |
PO |
525KHz |
1620KHz |
|
Ondes Courtes |
OC |
1620KHz |
30MHz |
|
FM |
Modulation de fréquences |
FM |
87,5MHz |
108MHz |
En radioélectricité, on préfère parler en longueur d'onde. Cette longueur \(\lambda\) est la distance parcourue par un onde électromagnétique à la vitesse \(c\) pendant une période \(T = 1/f\).
La vitesse \(c\) dépend du milieu. Dans le vide \(c \simeq 3 . 10^8 m/s\). C'est cette valeur qui sera retenue pour nos calculs. Donc \(\lambda = c/f\) et la formule Thomson devient :
\( \displaystyle \lambda_m=1.885 \sqrt{L_{\mu H}C_{pF}}\) ou encore \( \displaystyle f_{MHz}=\frac {159} { \sqrt{L_{\mu H}C_{pF}}}\)
Petites Ondes(PO).
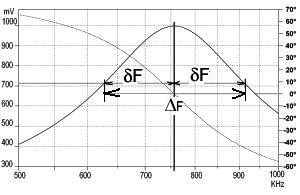 fig.4
fig.4
La bande passante vaut \(\Delta f= f_0/Q\). L'auditeur du poste TSF n'entendra que les signaux situés à droite (ou à gauche mais pas les deux) de la porteuse \(f_0\). La bande audible sera donc \(\Delta f=4.5KHz\). L'étroitesse de cette bande caractérise la sonorité typique de la gamme AM.
Sources et références
[1] Paul BERCHE, "Pratique et théorie de la TSF", Librairie de la Radio, Paris, 1937, revue par Roger RAFFIN, 1958.
[2] Lucien CHRETIEN, "Théorie et Pratique de la Radioélectricité", Editions Chiron, Paris, 1933.
[3] Jean QUINET, "Théorie & pratique des circuits électroniques" T.1, Ed. DUNOD, 1968.
[4] F. E. TERMAN, "Radio Engineer's Handbook", McGraw-Hill, New York, 1943.
