le montage Audion de base
Le schéma ci-contre illustre le principe de la détection directe par grille. Les deux bobines de gauche ainsi que condensateur variable de 500 cm constituent le bloc d’accord. La cellule composée de la résistance de 2 MΩ en parallèle avec un condensateur de 250 cm est le cœur de la détection directe. La triode détecte le signal HF issu du bloc d’accord. La self de choc constituée de 300 spires filtre la composante HF afin qu’elle ne parvienne pas à l’alimentation 60V.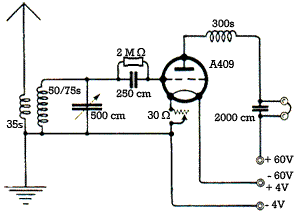
le montage Audion à réaction capacitive
Le schéma ci-contre illustre le principe de la détection directe par grille. Les deux bobines de gauche ainsi que condensateur variable de 500 cm constituent le bloc d’accord. La cellule composée de la résistance de 2 MΩ en parallèle avec un condensateur de 250 cm est le cœur de la détection directe. La triode détecte le signal HF issu du bloc d’accord. La self de choc constituée de 300 spires filtre la composante HF afin qu’elle ne parvienne pas à l’alimentation 60V.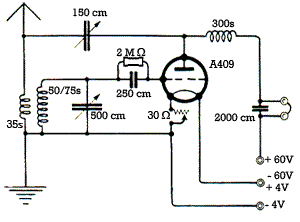
Expérimentation du montage Audion de base
calculette RLC
C'est après avoir extrait d'un radio-réveil HS le CV et le transformateur d'accord qu'on peut apercevoir sur la photo ci-dessous que m'est venue l'idée d'expérimenter le principe de la détection par grille. Les mesures sur ces 2 composants donnent
L'application de la formule de Thomson \(\displaystyle f_0=\frac {1}{2\pi \sqrt{LC}}\) avec \(\lambda_0=\frac {c}{f_0}\) montre que de la gamme GO pourra être captée.
L'expérimentation qui suit s'appuie sur un montage décrit dans le Berché ( Pratique et Théorie de la TSF) montré ici.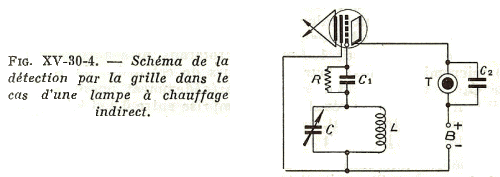
(Fig. 1)
Je me propose de passer le schéma de principe du montage à l'épreuve de SPICE.
Personnellement, j'utilise un outil gratuit de Linear Technologie que je trouve simple, souple et surtout sans limite commerciale. On le télécharge ici LTspice/SwitcherCAD III (4MB)
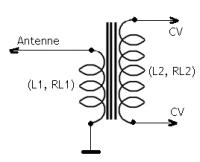
| L1 | RL1 | L2 | RL2 | CVmin | CVmax |
| 73 µH | 2,66 Ω | 7 530 µH | 24 Ω | 18 pF | 155 pF |
L'application de la formule de Thomson \(\displaystyle f_0=\frac {1}{2\pi \sqrt{LC}}\) avec \(\lambda_0=\frac {c}{f_0}\) montre que de la gamme GO pourra être captée.
| L2 | CV | \(f_0\) | \(l\) |
| 7 530 µH | 18 pF | 432 301 Hz | 694 m |
| 7 530 µH | 155 pF | 147 318 Hz | 2 036 m |
L'expérimentation qui suit s'appuie sur un montage décrit dans le Berché ( Pratique et Théorie de la TSF) montré ici.
(Fig. 1)
Je me propose de passer le schéma de principe du montage à l'épreuve de SPICE.
Personnellement, j'utilise un outil gratuit de Linear Technologie que je trouve simple, souple et surtout sans limite commerciale. On le télécharge ici LTspice/SwitcherCAD III (4MB)
Berché préconise \(100pF < C1 <150pF\) et \(200K\Omega < R < 500K\Omega\). Ces encadrements limites proviennent de considérations sur une faible distorsion BF si la condition ci-dessous est respectée.
Je choisis provisoirement C1=120pF et
R=330KΩ. L'écouteur dont je dispose est donné
pour 1KΩ. Après mesure de L=0,5H et Rsérie=1KΩ
. La capacité C2 est fixée grossièrement à 2nF.
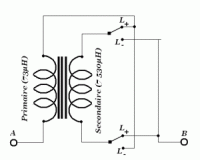
Reste à définir le transformateur HF. SPICE nécessite la connaissance de (\(L_1\), \(R_1\)), (\(L_2\), \(R_2\))et \(k\) le coefficient de couplage entre \(L_1\) et \(L_2\).
Le montage ci-dessous permet de mesurer les inductances \(L_{AB+}\) et\( L_{AB-}>\) du montage de la figure ci-contre, puis de déterminer le coefficient d'inductance mutuelle \(M\) et donc le coefficient de couplage \(k\). $$\begin{cases}L_{AB}(+) = L_1+L_2+2M=8.70mH\\L_{AB}(-)= L_1+L_2-2M=6.48mH\end{cases}$$ $$M=\frac {L_{AB}(+) +L_{AB}(-) }{4}=\frac {2.22}{4}=0.555mH$$ sachant que $$M=k\sqrt{L_1L_2}$$ On tire $$k=\frac {M}{\sqrt{L_1L_2}}=\frac {0.55}{\sqrt{0.073\times 7.52}}=0.748573$$
Le montage ci-dessous permet de mesurer les inductances \(L_{AB+}\) et\( L_{AB-}>\) du montage de la figure ci-contre, puis de déterminer le coefficient d'inductance mutuelle \(M\) et donc le coefficient de couplage \(k\). $$\begin{cases}L_{AB}(+) = L_1+L_2+2M=8.70mH\\L_{AB}(-)= L_1+L_2-2M=6.48mH\end{cases}$$ $$M=\frac {L_{AB}(+) +L_{AB}(-) }{4}=\frac {2.22}{4}=0.555mH$$ sachant que $$M=k\sqrt{L_1L_2}$$ On tire $$k=\frac {M}{\sqrt{L_1L_2}}=\frac {0.55}{\sqrt{0.073\times 7.52}}=0.748573$$
Résumons les paramètres du transformateur HF qui seront fournis à SPICE :
(\(L_1 = 73 \mu H ,R_{L1} = 2,66 \Omega\)) et (\(L_2 = 7,52 \mu H, R_{L2} = 24 \Omega\) ) et \(k = 0,748573\)
(\(L_1 = 73 \mu H ,R_{L1} = 2,66 \Omega\)) et (\(L_2 = 7,52 \mu H, R_{L2} = 24 \Omega\) ) et \(k = 0,748573\)
Antenne fictive
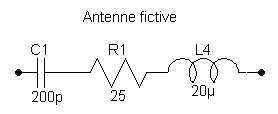
Pour attaquer le primaire de
ce transformateur, on utilisera un générateur HF en série avec une antenne
fictive constituée d'un circuit RLC série bien connu des radioamateurs. Un
autre modèle d'antenne fictive est donné ailleurs
Le schéma de simulation sera donc
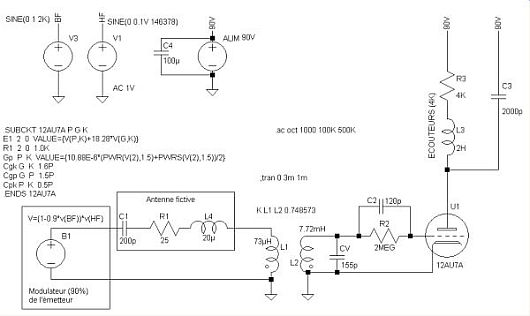
Le courant dans le secondaire du transformateur varie avec la fréquence comme suit
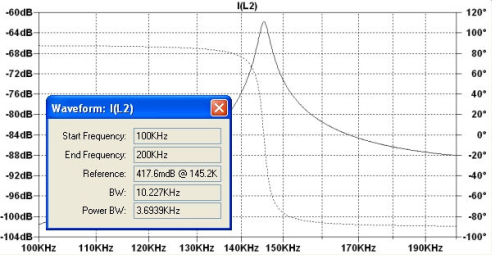
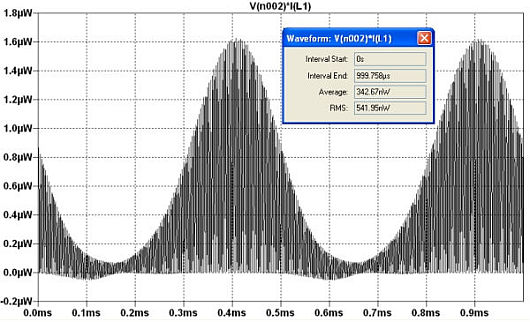
A la fréquence de résonance (145,2KHz), la puissance su signal dans le primaire du transformateur est de l'ordre de 0,55µW
La tension Grille de la triode est montrée
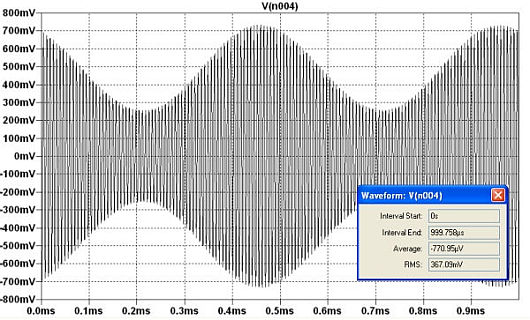
A comparer à la puissance absorbée par la grille
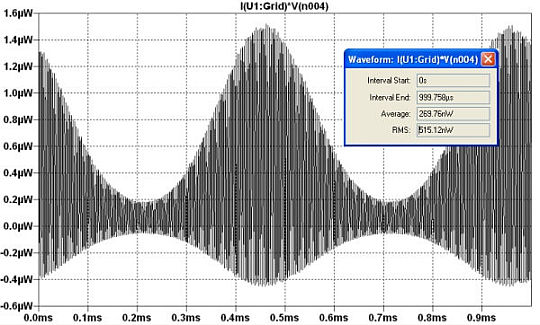
Le bilan de puissance est illustré par
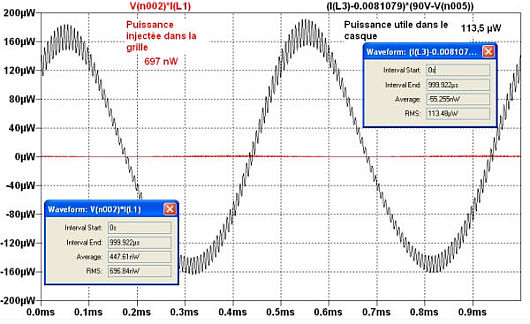
Le gain en puissance est \(\displaystyle G(dB)=10\log\frac {113.5}{0.697}=22.12dB\)
Sources et références
[1] Paul BERCHE, "Pratique et théorie de la TSF", Librairie de la Radio, Paris, 1937, revue par Roger RAFFIN, 1958.
[2] Lucien CHRETIEN, "Théorie et Pratique de la Radioélectricité", Editions Chiron, Paris, 1933.
